Stationäre Zustände des Elektrons im H-Atom

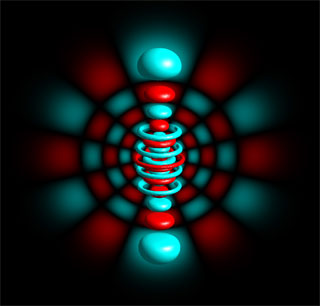
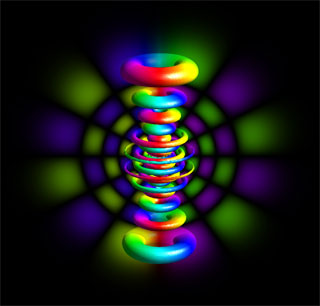
			Stationäre Zustände im Wasserstoffatom mit den magnetischen Quantenzahlen m=0,1,2,3,4,5 und 6.

Hier zeigen wir einige der vielfältigen stationären Wellenfunktionen, die die verschiedenen möglichen Zustände eines Elektrons im Wasserstoffatom beschreiben. Die Visualisierung kombiniert eine Isofläche des Betrags, um die dreidimensionale Form anzudeuten, mit einer (transparenten) Querschnittfläche, die den unscharfen Verlauf der Intensität anzeigt. Auf dieser Querschnittfläche ist die Lage der Nullstellen gut erkennbar.

Alle diese Zustände beschreiben ein Elektron mit derselben Energie, aber unterschiedlichen Drehimpulsen um die z-Achse. Die Wellenfunktion im ersten Bild hat ihre größte Amplitude nahe bei der z-Achse. Diese "stangenförmige" Ortsverteilung hat den geringsten Drehimpuls um die z-Achse. Das letzte Bild zeigt eine flach ausgebreitete, "scheibenförmige" Ortsverteilung. Diese hat den größten Drehimpuls um die z-Achse.

Zwischen diesen beiden Extremen gibt es nur die gezeigten Möglichkeiten für stationäre Wellenfunktionen. Man sagt, der Drehimpuls um die z-Achse ist quantisiert. Man beschreibt das durch die Quantenzahl m, die die obigen Bilder durchnummeriert. Bei der gezeigten Energie kann der Drehimpuls um die z-Achse nur die Quantenzahlen m=0, 1, 2, 3, 4, 5, 6 haben. Die Quantenzahl m misst auch die Anzahl der Wellenlängen, die auf jedem Ring Platz haben.

< zurück | weiter >

Links: